Well-quasi-ordering
In mathematics, specifically order theory, a well-quasi-ordering or wqo is a well-founded quasi-ordering with an additional restriction on sequences - that there is no infinite sequence  with
with 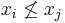 for all
for all 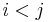 .
.
Contents |
Motivation
We can use well-founded induction on any set with a well-founded relation, thus one is interested in when a quasi-order is well-founded. However the class of well-founded quasiorders is not closed under certain operations - that is, when we use a quasi-order to obtain a new quasi-order on a set of structures derived from our original set, we find this quasiorder is not well-founded. By placing stronger restrictions on the original well-founded quasiordering one can hope to ensure that our derived quasiorderings are still well-founded.
An example of this is the power set operation. Given a quasiordering 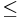 for a set
for a set  we can define a quasiorder
we can define a quasiorder 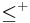 on
on  's power set
's power set 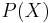 by setting
by setting 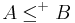 if and only if for each element of
if and only if for each element of  we can find some element of
we can find some element of  which is larger than it under
which is larger than it under 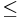 . We find that this quasiordering on
. We find that this quasiordering on 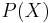 needn't be well-founded but that if we took our original quasi-ordering to be a well-quasi-ordering then it is.
needn't be well-founded but that if we took our original quasi-ordering to be a well-quasi-ordering then it is.
Formal definition
A well-quasi-ordering on a set  is a quasi-ordering in which (i.e., a reflexive, transitive binary relation) such that any infinite sequence of elements
is a quasi-ordering in which (i.e., a reflexive, transitive binary relation) such that any infinite sequence of elements 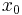 ,
, 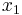 ,
, 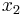 , … from
, … from  contains an increasing pair
contains an increasing pair  ≤
≤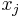 with
with  <
< . The set
. The set  is said to be well-quasi-ordered, or shortly wqo.
is said to be well-quasi-ordered, or shortly wqo.
A well partial order, or a wpo, is a wqo that is a proper ordering relation, i.e., it is antisymmetric.
Among other ways of defining wqo's, one is to say that they do not contain infinite strictly decreasing sequences (of the form 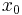 >
>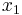 >
>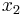 >…) nor infinite sequences of pairwise incomparable elements. Hence a quasi-order (
>…) nor infinite sequences of pairwise incomparable elements. Hence a quasi-order ( ,≤) is wqo if and only if it is well-founded and has no infinite antichains.
,≤) is wqo if and only if it is well-founded and has no infinite antichains.
Examples
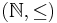 , the set of natural numbers with standard ordering, is a well partial order.
, the set of natural numbers with standard ordering, is a well partial order. 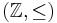 , the set of positive and negative integers, is not: it is not well-founded.
, the set of positive and negative integers, is not: it is not well-founded.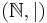 , the set of natural numbers ordered by divisibility, is not a well partial order: the prime numbers are an infinite antichain.
, the set of natural numbers ordered by divisibility, is not a well partial order: the prime numbers are an infinite antichain.- The set of words ordered lexicographically, i.e., as in a dictionary, is not a wqo: it is not well-founded as witnessed by the decreasing sequence
 ,
, 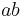 ,
, 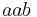 ,
, 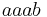 , ... If we consider the prefix ordering for comparing words, then the previous sequence becomes an infinite antichain.
, ... If we consider the prefix ordering for comparing words, then the previous sequence becomes an infinite antichain. 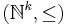 , the set of vectors of
, the set of vectors of  natural numbers with component-wise ordering, is a well partial order (Dickson's lemma). More generally, if
natural numbers with component-wise ordering, is a well partial order (Dickson's lemma). More generally, if 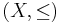 is wqo, then for any
is wqo, then for any  ,
, 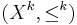 is wqo.
is wqo.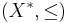 , the set of finite
, the set of finite  -sequences ordered by embedding is a wqo if and only if
-sequences ordered by embedding is a wqo if and only if 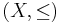 is (Higman's lemma). Recall that one embeds a sequence
is (Higman's lemma). Recall that one embeds a sequence  into a sequence
into a sequence  by finding a subsequence of
by finding a subsequence of  that has the same length as
that has the same length as  and that dominates it term by term. When
and that dominates it term by term. When 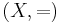 is a finite unordered set,
is a finite unordered set, 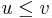 if and only if
if and only if  is a subsequence of
is a subsequence of  .
.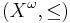 , the set of infinite sequences over a wqo
, the set of infinite sequences over a wqo 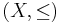 , ordered by embedding is not a wqo in general. That is, Higman's lemma does not carry over to infinite sequences. Better-quasi-orderings have been introduced to generalize Higman's lemma to sequences of arbitrary lengths.
, ordered by embedding is not a wqo in general. That is, Higman's lemma does not carry over to infinite sequences. Better-quasi-orderings have been introduced to generalize Higman's lemma to sequences of arbitrary lengths.- Embedding between finite trees with nodes labeled by elements of a wqo
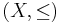 is a wqo (Kruskal's tree theorem).
is a wqo (Kruskal's tree theorem). - Embedding between infinite trees with nodes labeled by elements of a wqo
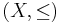 is a wqo (Nash-Williams' theorem).
is a wqo (Nash-Williams' theorem). - Embedding between countable scattered linear order types is a wqo (Laver's theorem).
- Embedding between countable boolean algebras is a wqo. This follows from Laver's theorem and a theorem of Ketonen.
- Finite graphs ordered by a notion of embedding called "graph minor" is a wqo (Robertson–Seymour theorem).
Wqo's versus well partial orders
In practice, the wqo's one manipulates are almost always orderings (see examples above), but the theory is technically smoother if we do not require antisymmetry, so it is built with wqo's as the basic notion.
Observe that a wpo is a wqo, and that a wqo gives rise to a wpo between equivalence classes induced by the kernel of the wqo. For example, if we order 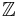 by divisibility, we end up with
by divisibility, we end up with 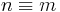 if and only if
if and only if 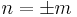 , so that
, so that 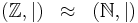 .
.
Infinite increasing subsequences
If ( , ≤) is wqo then every infinite sequence
, ≤) is wqo then every infinite sequence 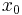 ,
, 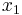 ,
, 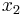 , … contains an infinite increasing subsequence
, … contains an infinite increasing subsequence 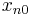 ≤
≤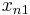 ≤
≤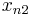 ≤… (with
≤… (with 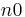 <
<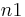 <
<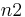 <…). Such a subsequence is sometimes called perfect. This can be proved by a Ramsey argument: given some sequence
<…). Such a subsequence is sometimes called perfect. This can be proved by a Ramsey argument: given some sequence 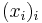 , consider the set
, consider the set  of indexes
of indexes  such that
such that  has no larger or equal
has no larger or equal 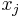 to its right, i.e., with
to its right, i.e., with 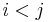 . If
. If  is infinite, then the
is infinite, then the  -extracted subsequence contradicts the assumption that
-extracted subsequence contradicts the assumption that  is wqo. So
is wqo. So  is finite, and any
is finite, and any 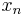 with
with  larger than any index in
larger than any index in  can be used as the starting point of an infinite increasing subsequence.
can be used as the starting point of an infinite increasing subsequence.
The existence of such infinite increasing subsequences is sometimes taken as a definition for well-quasi-ordering, leading to an equivalent notion.
Properties of wqos
- Given a quasiordering
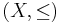 the quasiordering
the quasiordering 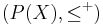 defined by
defined by 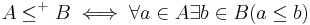 is well-founded if and only if
is well-founded if and only if 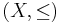 is a wqo.
is a wqo. - A quasiordering is a wqo if and only if the corresponding partial order (obtained by quotienting by
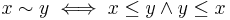 ) has no infinite descending sequences or antichains. (This can be proved using a Ramsey argument as above)
) has no infinite descending sequences or antichains. (This can be proved using a Ramsey argument as above)
References
- Dickson, L. E. (1913). "Finiteness of the odd perfect and primitive abundant numbers with
 distinct prime factors". Amer. Journal Math. (American Journal of Mathematics, Vol. 35, No. 4) 35 (4): 413–422. doi:10.2307/2370405. JSTOR 2370405.
distinct prime factors". Amer. Journal Math. (American Journal of Mathematics, Vol. 35, No. 4) 35 (4): 413–422. doi:10.2307/2370405. JSTOR 2370405. - Higman, G. (1952). "Ordering by divisibility in abstract algebras". Proc. London Math. Soc., 3rd series 2: 326–336. doi:10.1112/plms/s3-2.1.326.
- Kruskal, J. B. (1972). "The theory of well-quasi-ordering: A frequently discovered concept". Journal of Combinatorial Theory, Series A 13 (3): 297–305. doi:10.1016/0097-3165(72)90063-5.
- Ketonen, Jussi (1978). "The structure of countable Boolean algebras". Annals of Mathematics (The Annals of Mathematics, Vol. 108, No. 1) 108 (1): 41–89. doi:10.2307/1970929. JSTOR 1970929.
- Milner, E. C. (1985). "Basic WQO- and BQO-theory". In I. Rival (ed.). Graphs and Order. The Role of Graphs in the Theory of Ordered Sets and Its Applications. D. Reidel Publishing Co.. pp. 487–502. ISBN 90-277-1943-8.
- Gallier, Jean H. (1991). "What's so special about Kruskal's theorem and the ordinal Γo? A survey of some results in proof theory". Annals of Pure and Applied Logic 53 (3): 199–260. doi:10.1016/0168-0072(91)90022-E.